帕斯卡定理#
(该定理曾由XGJ同学用建系的方法证明,故又称为XGJ大定理)
帕斯卡定理,指任何圆锥曲线内接六边形(包括退化的六边形,比如有六个点的四边形)其三个对边的交点共线。为了研究方便,我们只研究在圆中的情况。
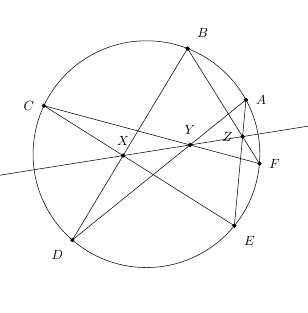 如上图,$X、Y、Z$三点共线。
如上图,$X、Y、Z$三点共线。
帕斯卡定理的证明#
为了更好地讲述帕斯卡定理的证明,我们要先来了解一个定理。
梅涅劳斯定理#
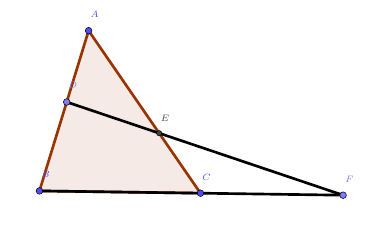 如上图,若$D、E、F$三点共线,则有$\frac{AD}{DB}\cdot\frac{BF}{CF}\cdot\frac{CE}{EA}=1$,此时我们称三角形$ABC$为梅氏三角形,$DEF$为梅氏线。
如上图,若$D、E、F$三点共线,则有$\frac{AD}{DB}\cdot\frac{BF}{CF}\cdot\frac{CE}{EA}=1$,此时我们称三角形$ABC$为梅氏三角形,$DEF$为梅氏线。
证明:
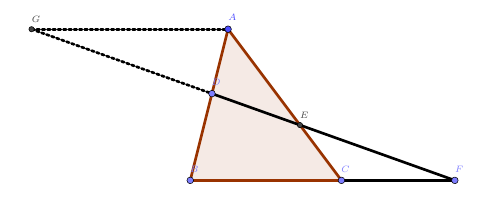 过点$A$作$AG//BC$交$FD$延长线于$G$。
易得$\triangle AGD\sim\triangle BFD,\triangle AGE\sim\triangle CFE$,
$\therefore \frac{AD}{DB}=\frac{AG}{BF},\frac{CE}{EA}=\frac{CF}{AG}$,
$\therefore \frac{AD}{DB}\cdot\frac{BF}{CF}\cdot\frac{CE}{EA}=\frac{AG}{BF}\cdot\frac{CF}{AG}\cdot\frac{BF}{CF}=1$,证毕。
过点$A$作$AG//BC$交$FD$延长线于$G$。
易得$\triangle AGD\sim\triangle BFD,\triangle AGE\sim\triangle CFE$,
$\therefore \frac{AD}{DB}=\frac{AG}{BF},\frac{CE}{EA}=\frac{CF}{AG}$,
$\therefore \frac{AD}{DB}\cdot\frac{BF}{CF}\cdot\frac{CE}{EA}=\frac{AG}{BF}\cdot\frac{CF}{AG}\cdot\frac{BF}{CF}=1$,证毕。
梅涅劳斯定理逆定理#
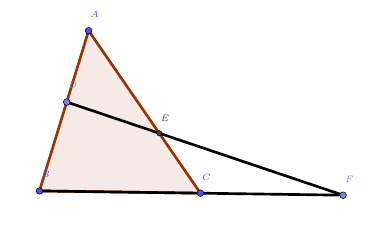 还是这张图,如果能满足$\frac{AD}{DB}\cdot\frac{BF}{CF}\cdot\frac{CE}{EA}=1$,则能得到$D、E、F$三点共线。该结论使用同一法即可证明,不再赘述。
还是这张图,如果能满足$\frac{AD}{DB}\cdot\frac{BF}{CF}\cdot\frac{CE}{EA}=1$,则能得到$D、E、F$三点共线。该结论使用同一法即可证明,不再赘述。
证明方法一:梅涅劳斯定理法#
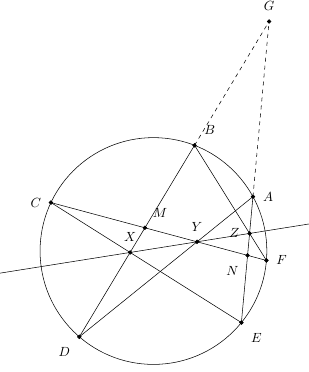 延长$DB$和$EA$交于点$G$,记$CF$和$BD$交于点$M$,$AE$和$CF$交于$N$。
我们要证$X、Y、Z$三点共线,只要证明$\frac{GX}{XM}\cdot\frac{MY}{YN}\cdot\frac{NZ}{ZG}=1$,
我们以$\triangle GMN$为梅氏三角形,分别以$BZF、AYD、CXE$为梅氏线运用梅涅劳斯定理,可以得到三个式子:
$$\frac{GB}{BM}\cdot\frac{MF}{FN}\cdot\frac{NZ}{ZG}=1 \rightarrow \frac{NZ}{ZG}=\frac{BM}{GB}\cdot\frac{FN}{MF}$$
$$\frac{GD}{DM}\cdot\frac{MY}{YN}\cdot\frac{NA}{AG}=1 \rightarrow \frac{MY}{YN}=\frac{DM}{GD}\cdot\frac{AG}{NA}$$
$$\frac{GX}{XM}\cdot\frac{MC}{CN}\cdot\frac{NE}{EG}=1 \rightarrow \frac{GX}{XM}=\frac{CN}{MC}\cdot\frac{EG}{NE}$$
上面三个式子相乘,可以得到
$$\frac{GX}{XM}\cdot\frac{MY}{YN}\cdot\frac{NZ}{ZG}=\frac{(GA\cdot GE)(BM\cdot DM)(CN\cdot FN)}{(GB\cdot GD)(MC\cdot MF)(NA\cdot NE)}$$
由圆幂定理可以知道$GA\cdot GE=GB\cdot GD,BM\cdot DM=MC\cdot MF,CN\cdot FN=NA\cdot NE$
于是便有$\frac{GX}{XM}\cdot\frac{MY}{YN}\cdot\frac{NZ}{ZG}=1$,证毕。
延长$DB$和$EA$交于点$G$,记$CF$和$BD$交于点$M$,$AE$和$CF$交于$N$。
我们要证$X、Y、Z$三点共线,只要证明$\frac{GX}{XM}\cdot\frac{MY}{YN}\cdot\frac{NZ}{ZG}=1$,
我们以$\triangle GMN$为梅氏三角形,分别以$BZF、AYD、CXE$为梅氏线运用梅涅劳斯定理,可以得到三个式子:
$$\frac{GB}{BM}\cdot\frac{MF}{FN}\cdot\frac{NZ}{ZG}=1 \rightarrow \frac{NZ}{ZG}=\frac{BM}{GB}\cdot\frac{FN}{MF}$$
$$\frac{GD}{DM}\cdot\frac{MY}{YN}\cdot\frac{NA}{AG}=1 \rightarrow \frac{MY}{YN}=\frac{DM}{GD}\cdot\frac{AG}{NA}$$
$$\frac{GX}{XM}\cdot\frac{MC}{CN}\cdot\frac{NE}{EG}=1 \rightarrow \frac{GX}{XM}=\frac{CN}{MC}\cdot\frac{EG}{NE}$$
上面三个式子相乘,可以得到
$$\frac{GX}{XM}\cdot\frac{MY}{YN}\cdot\frac{NZ}{ZG}=\frac{(GA\cdot GE)(BM\cdot DM)(CN\cdot FN)}{(GB\cdot GD)(MC\cdot MF)(NA\cdot NE)}$$
由圆幂定理可以知道$GA\cdot GE=GB\cdot GD,BM\cdot DM=MC\cdot MF,CN\cdot FN=NA\cdot NE$
于是便有$\frac{GX}{XM}\cdot\frac{MY}{YN}\cdot\frac{NZ}{ZG}=1$,证毕。
共角定理#
上面的证明貌似能够证明所有的情况,但是接下来就是一个反例!
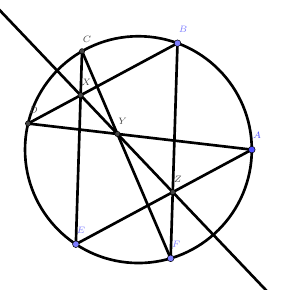 上图中,$CE//BF$,$BD//AE$,也就是说延长线段构造梅氏三角形的方法不适用了!我们该何去何从?
我们需要换另外一种证明方法,在那之前我们要了解另外一个简单的定理。
共角定理
上图中,$CE//BF$,$BD//AE$,也就是说延长线段构造梅氏三角形的方法不适用了!我们该何去何从?
我们需要换另外一种证明方法,在那之前我们要了解另外一个简单的定理。
共角定理
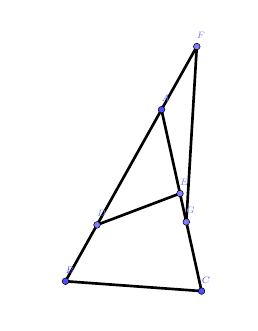 两个三角形有一对角相等或互补时,其面积之比等于其角的两边乘积之比,例如上图中就有:
$$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=\frac{AD\cdot AE}{AB\cdot AC}$$
$$\frac{S_{\triangle AFG}}{S_{\triangle ABC}}=\frac{AF\cdot AG}{AB\cdot AC}$$
证明也非常简单,只要用三角形面积公式$S_\triangle=\frac{1}{2}ab\sin C$就行了。
两个三角形有一对角相等或互补时,其面积之比等于其角的两边乘积之比,例如上图中就有:
$$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=\frac{AD\cdot AE}{AB\cdot AC}$$
$$\frac{S_{\triangle AFG}}{S_{\triangle ABC}}=\frac{AF\cdot AG}{AB\cdot AC}$$
证明也非常简单,只要用三角形面积公式$S_\triangle=\frac{1}{2}ab\sin C$就行了。
证明方法二:面积法#
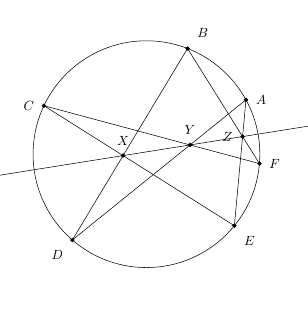 为了证明$X、Y、Z$三点共线,我们只需要证明$CF、AD、XZ$三线共点就行了。如何证明?我们采用同一法。
为了证明$X、Y、Z$三点共线,我们只需要证明$CF、AD、XZ$三线共点就行了。如何证明?我们采用同一法。
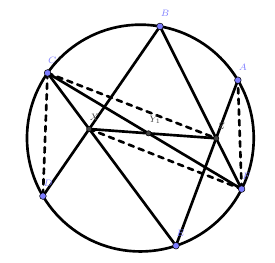
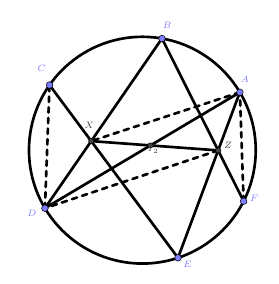 由上面两张图,我们只需要证明$\frac{XY_1}{Y_1Z}=\frac{XY_2}{Y_2Z}$
如上面两张图作辅助线。
$$\frac{XY_1}{Y_1Z}=\frac{S_{\triangle XCF}}{S_{\triangle ZCF}}=\frac{S_{\triangle XCF}}{S_{\triangle AZF}}\cdot\frac{S_{\triangle DCX}}{S_{\triangle ZCF}}\cdot\frac{S_{\triangle AZF}}{S_{\triangle DCX}}$$
因为$\angle XCF=\angle ZAF$,运用共角定理可知$\frac{S_{\triangle XCF}}{S_{\triangle AZF}}=\frac{XC\cdot CF}{AZ\cdot AF}$,同理可知$\frac{S_{\triangle DCX}}{S_{\triangle ZCF}}=\frac{CD\cdot DX}{CF\cdot ZF}$,于是有
$$\frac{XY_1}{Y_1Z}=\frac{XC\cdot CF}{AZ\cdot AF}\cdot\frac{CD\cdot DX}{CF\cdot ZF}\cdot\frac{S_{\triangle AZF}}{S_{\triangle DCX}}=\frac{XC\cdot CD\cdot DX}{AZ\cdot ZF \cdot FA}\cdot\frac{S_{\triangle AZF}}{S_{\triangle DCX}}$$
同理有
$$\frac{XY_2}{Y_2Z}=\frac{S_{\triangle DXA}}{S_{\triangle DZA}}=\frac{S_{\triangle DXA}}{S_{\triangle FAZ}}\cdot\frac{S_{\triangle DCX}}{S_{\triangle DZA}}\cdot\frac{S_{\triangle AZF}}{S_{\triangle DCX}}=$$
$$\frac{DA\cdot DX}{FZ\cdot FA}\cdot\frac{DC\cdot CX}{DA\cdot AZ}\cdot\frac{S_{\triangle AZF}}{S_{\triangle DCX}}=\frac{DC\cdot CX\cdot DX}{AZ\cdot ZF\cdot AF}\cdot\frac{S_{\triangle AZF}}{S_{\triangle DCX}}$$
上下两式相等,$\frac{XY_1}{Y_1Z}=\frac{XY_2}{Y_2Z}$,命题得证。
由上面两张图,我们只需要证明$\frac{XY_1}{Y_1Z}=\frac{XY_2}{Y_2Z}$
如上面两张图作辅助线。
$$\frac{XY_1}{Y_1Z}=\frac{S_{\triangle XCF}}{S_{\triangle ZCF}}=\frac{S_{\triangle XCF}}{S_{\triangle AZF}}\cdot\frac{S_{\triangle DCX}}{S_{\triangle ZCF}}\cdot\frac{S_{\triangle AZF}}{S_{\triangle DCX}}$$
因为$\angle XCF=\angle ZAF$,运用共角定理可知$\frac{S_{\triangle XCF}}{S_{\triangle AZF}}=\frac{XC\cdot CF}{AZ\cdot AF}$,同理可知$\frac{S_{\triangle DCX}}{S_{\triangle ZCF}}=\frac{CD\cdot DX}{CF\cdot ZF}$,于是有
$$\frac{XY_1}{Y_1Z}=\frac{XC\cdot CF}{AZ\cdot AF}\cdot\frac{CD\cdot DX}{CF\cdot ZF}\cdot\frac{S_{\triangle AZF}}{S_{\triangle DCX}}=\frac{XC\cdot CD\cdot DX}{AZ\cdot ZF \cdot FA}\cdot\frac{S_{\triangle AZF}}{S_{\triangle DCX}}$$
同理有
$$\frac{XY_2}{Y_2Z}=\frac{S_{\triangle DXA}}{S_{\triangle DZA}}=\frac{S_{\triangle DXA}}{S_{\triangle FAZ}}\cdot\frac{S_{\triangle DCX}}{S_{\triangle DZA}}\cdot\frac{S_{\triangle AZF}}{S_{\triangle DCX}}=$$
$$\frac{DA\cdot DX}{FZ\cdot FA}\cdot\frac{DC\cdot CX}{DA\cdot AZ}\cdot\frac{S_{\triangle AZF}}{S_{\triangle DCX}}=\frac{DC\cdot CX\cdot DX}{AZ\cdot ZF\cdot AF}\cdot\frac{S_{\triangle AZF}}{S_{\triangle DCX}}$$
上下两式相等,$\frac{XY_1}{Y_1Z}=\frac{XY_2}{Y_2Z}$,命题得证。
帕斯卡定理的退化及其应用#
文章的一开头我们就说了,任何的六边形,不管是什么首尾连接方式,不管是什么退化,都能满足帕斯卡定理,因此这是一个很强的定理,在证明三点共线时会遇见它。
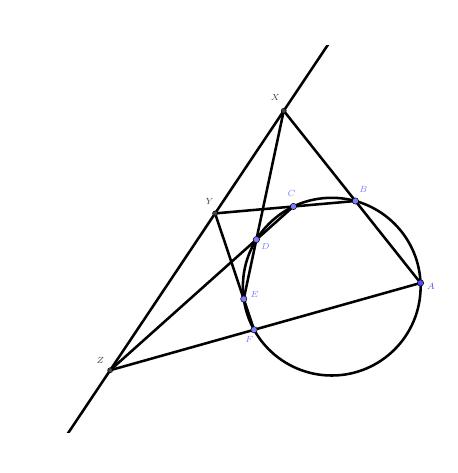
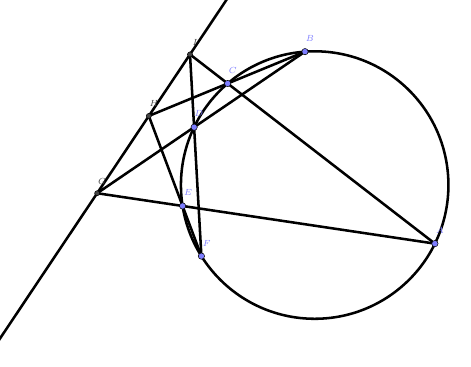 这两个都是帕斯卡定理在形外的版本。
这两个都是帕斯卡定理在形外的版本。
题目描述
尝试证明以上两个帕斯卡定理的变形。
提示
对照上面的证明方法,形变而法不变!
不过,如果六边形退化了呢?
当两个点不断接近,直到最终重合时,两点间的连线就会退化为切线,如下图:
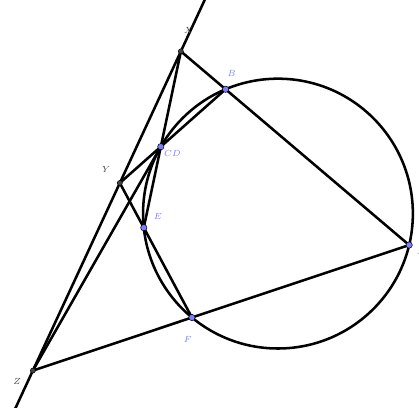 其中$CZ$ 为圆的切线,可以发现$X、Y、Z$仍然三点共线。同理,其他的点也可以逐一重合,图形不断退化,因此即便一个看似普通的三点共线,也有可能是帕斯卡定理的退化!
题目
设$H$是锐角$\triangle ABC$的垂心,$M$是$BC$的中点,以$AH$为直径作圆与AB、AC分别交于点$D、E$,$AH$交$DE$于$P$,过$H$作$AH$的垂线交$DM$于点$Q$,求证:$P、Q、B$三点共线。
其中$CZ$ 为圆的切线,可以发现$X、Y、Z$仍然三点共线。同理,其他的点也可以逐一重合,图形不断退化,因此即便一个看似普通的三点共线,也有可能是帕斯卡定理的退化!
题目
设$H$是锐角$\triangle ABC$的垂心,$M$是$BC$的中点,以$AH$为直径作圆与AB、AC分别交于点$D、E$,$AH$交$DE$于$P$,过$H$作$AH$的垂线交$DM$于点$Q$,求证:$P、Q、B$三点共线。
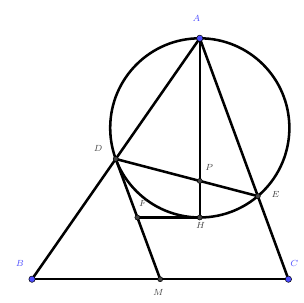
提示
有两条切线。
思路
证明 DQ 和 HQ 是两条切线,即可对圆内接六边形ADDHHE使用帕斯卡定理。




 延长$DB$和$EA$交于点$G$,记$CF$和$BD$交于点$M$,$AE$和$CF$交于$N$。
我们要证$X、Y、Z$三点共线,只要证明$\frac{GX}{XM}\cdot\frac{MY}{YN}\cdot\frac{NZ}{ZG}=1$,
我们以$\triangle GMN$为梅氏三角形,分别以$BZF、AYD、CXE$为梅氏线运用梅涅劳斯定理,可以得到三个式子:
$$\frac{GB}{BM}\cdot\frac{MF}{FN}\cdot\frac{NZ}{ZG}=1 \rightarrow \frac{NZ}{ZG}=\frac{BM}{GB}\cdot\frac{FN}{MF}$$
$$\frac{GD}{DM}\cdot\frac{MY}{YN}\cdot\frac{NA}{AG}=1 \rightarrow \frac{MY}{YN}=\frac{DM}{GD}\cdot\frac{AG}{NA}$$
$$\frac{GX}{XM}\cdot\frac{MC}{CN}\cdot\frac{NE}{EG}=1 \rightarrow \frac{GX}{XM}=\frac{CN}{MC}\cdot\frac{EG}{NE}$$
上面三个式子相乘,可以得到
$$\frac{GX}{XM}\cdot\frac{MY}{YN}\cdot\frac{NZ}{ZG}=\frac{(GA\cdot GE)(BM\cdot DM)(CN\cdot FN)}{(GB\cdot GD)(MC\cdot MF)(NA\cdot NE)}$$
由圆幂定理可以知道$GA\cdot GE=GB\cdot GD,BM\cdot DM=MC\cdot MF,CN\cdot FN=NA\cdot NE$
于是便有$\frac{GX}{XM}\cdot\frac{MY}{YN}\cdot\frac{NZ}{ZG}=1$,证毕。
延长$DB$和$EA$交于点$G$,记$CF$和$BD$交于点$M$,$AE$和$CF$交于$N$。
我们要证$X、Y、Z$三点共线,只要证明$\frac{GX}{XM}\cdot\frac{MY}{YN}\cdot\frac{NZ}{ZG}=1$,
我们以$\triangle GMN$为梅氏三角形,分别以$BZF、AYD、CXE$为梅氏线运用梅涅劳斯定理,可以得到三个式子:
$$\frac{GB}{BM}\cdot\frac{MF}{FN}\cdot\frac{NZ}{ZG}=1 \rightarrow \frac{NZ}{ZG}=\frac{BM}{GB}\cdot\frac{FN}{MF}$$
$$\frac{GD}{DM}\cdot\frac{MY}{YN}\cdot\frac{NA}{AG}=1 \rightarrow \frac{MY}{YN}=\frac{DM}{GD}\cdot\frac{AG}{NA}$$
$$\frac{GX}{XM}\cdot\frac{MC}{CN}\cdot\frac{NE}{EG}=1 \rightarrow \frac{GX}{XM}=\frac{CN}{MC}\cdot\frac{EG}{NE}$$
上面三个式子相乘,可以得到
$$\frac{GX}{XM}\cdot\frac{MY}{YN}\cdot\frac{NZ}{ZG}=\frac{(GA\cdot GE)(BM\cdot DM)(CN\cdot FN)}{(GB\cdot GD)(MC\cdot MF)(NA\cdot NE)}$$
由圆幂定理可以知道$GA\cdot GE=GB\cdot GD,BM\cdot DM=MC\cdot MF,CN\cdot FN=NA\cdot NE$
于是便有$\frac{GX}{XM}\cdot\frac{MY}{YN}\cdot\frac{NZ}{ZG}=1$,证毕。







