三角形的内心

三角形的内心的性质

三角形的内心（一般用字母$I$表示)，是三角形内切圆的圆心，也是三角形三条角平分线的交点,如下图所示。

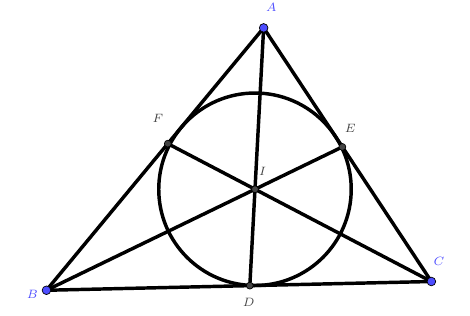
内心有什么特殊的性质呢？

性质1 在上图中，我们有$\angle BIC=90^\circ+\frac{1}{2}\angle BAC$，其余的同理。 性质2 在上图中，我们$AF=AE=\frac{b+c-a}{2},BF=BD=\frac{c+a-b}{2},CD=CE=\frac{a+b-c}{2}$，且$S_{\triangle ABC}=\frac{1}{2}(a+b+c)r$。 性质3 又被称作“鸡爪定理"，如下图。 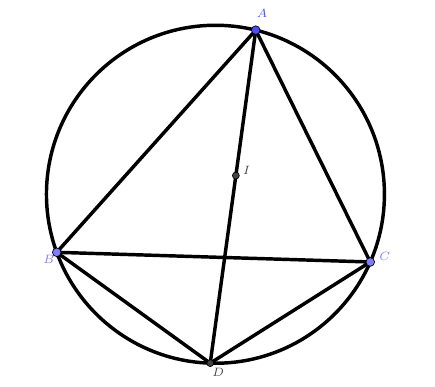设$I$为$\triangle ABC$内一点，$AI$所在直线交$\triangle ABC$的外接圆与$D$，$I$为$\triangle ABC$内心的充要条件是：$ID=BD=DC$。

以上是内心的最最基本的性质，不过用它们我们已经可以解决一些题目了。

内心性质的应用——导角、导边、相似与共圆

例题1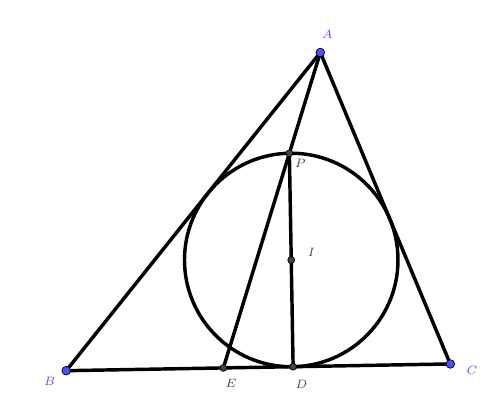： $\odot I$是$\triangle ABC$的内切圆，$D$为与$BC$的切点，延长$DI$交圆与$P$,再延长$AP$交$BC$与$E$，求证：$BQ=DC$。 Tips:除了内心的性质外，与切点有关的垂直、角平分线也是重要的条件啊！

证明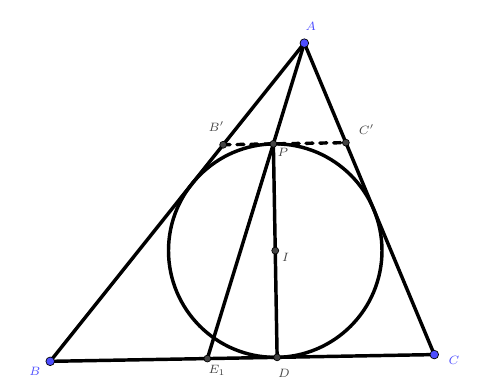： 过$P$作$B’C’//BC$分别交$AB$与$B’$，交$AC$与$C’$。 易知$B’C’$为$\odot I$切线，由$Rt\triangle PIC’\sim Rt\triangle DCI$有$PI\cdot ID=PC’\cdot DC$。 同理，$PI\cdot ID=B’P\cdot BD$，因此，我们有$\frac{B’P}{PC’}=\frac{DC}{BD}$。 由平行线的性质，我们有$\frac{B’P}{PC’}=\frac{BQ}{QC}$，因此$\frac{DC}{BD}=\frac{BQ}{QC}$，再由合比定理知$\frac{DC}{BC}=\frac{BQ}{BC}$，从而$DC=BQ$。证毕。

例题2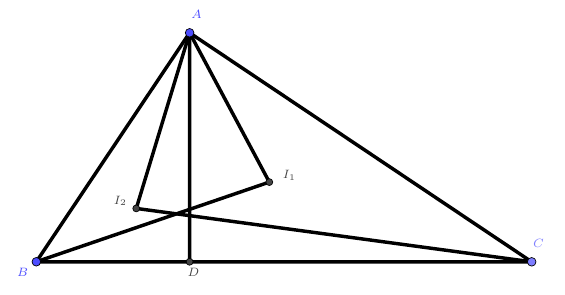： 在$Rt \triangle ABC$中，$\angle C=90^\circ$，$CD$是斜边上的高，$I_1$、$I_2$分别是$\triangle ADC$和$\triangle BCD$的内心。求证：$\angle AO_2C=\angle BO_1C$。 Tips：射影定理的基本图形，引出了许多相等的角。图中有一组四点共圆。

证明： 设$\angle ACD=\alpha$（方便导角）,则$\angle I_2BD=45^\circ-\frac{1}{2}\alpha,\angle DI_1C=135^\circ-\frac{1}{2}\alpha$。 易得$\triangle AI_2D\sim\triangle CI_1D$，则$\triangle I_2DI_1\sim\triangle ADC$，从而$\angle I_2I_1D=\alpha$。 则$\angle I_2BD+\angle I_2I_1C=45^\circ-\frac{1}{2}\alpha+135^\circ-\frac{1}{2}\alpha+\alpha=180^\circ$，即$B$、$I_2$、$I_1$、$C$四点共圆。 所以$\angle BI_2C=\angle BI_1C$。又因为$\angle AI_2B=\angle AI_1C=135^\circ$，所以$\angle AO_2C=\angle BO_1C$，证毕。

实际上，在上面那一道题的背景中，只要稍微连接几条线段，就有很多很多的相似三角形，详情见TYNFMS官网的奇怪页面。

内心性质的应用：利用三角函数的计算

例题1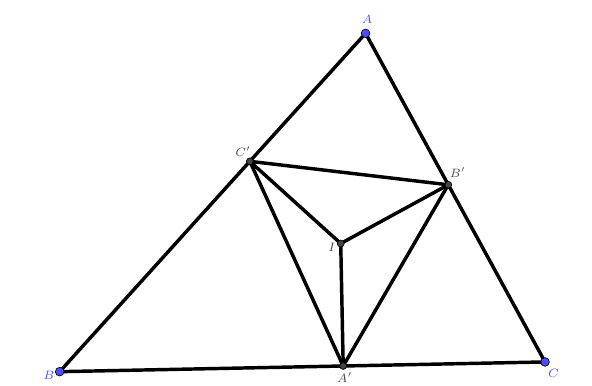： 设$I$是$\triangle ABC$的内心，$\triangle A’B’C’$是从$I’$向$BC$，$CA$，$AB$所作垂线的垂足三角形，证明：$\cot\angle A+\cot\angle B+\cot\angle C\geqslant\cot\angle A’+\cot\angle B’+\cot\angle C’$。

证明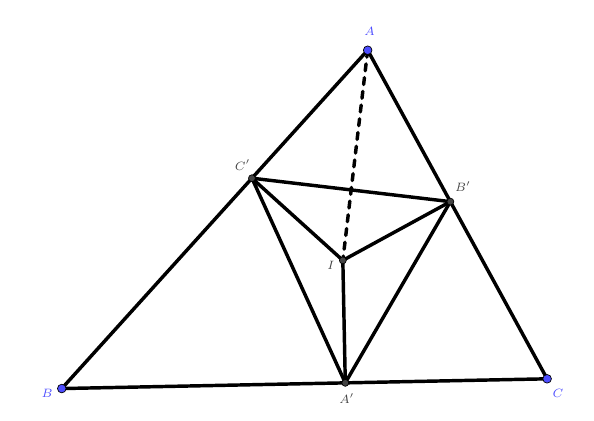： 连接$AI$，易得$\angle C’IA=\angle A’$，又因$AI\perp B’C’$，则$\cot A’=\tan C’AI=\tan\frac{1}{2}\angle A$。 因此，原不等式等价于$\cot\angle A+\cot\angle B+\cot\angle C\geqslant\tan\frac{1}{2}\angle A+\tan\frac{1}{2}\angle B+\tan\frac{1}{2}\angle C$。 因为$\cot\angle B+\cot\angle C=\frac{\sin(\angle B+\angle C)}{\sin\angle B\cdot\sin\angle C}=\frac{2\sin\angle A}{\cos(\angle B-\angle C)-\cos(\angle B+\angle C)}$ $=\frac{2\angle A}{\cos(\angle B-\angle C)+\cos\angle A}\geqslant\frac{2\sin\angle A}{1+\cos\angle A}=2\tan \frac{1}{2}\angle A$ 同理可得其他2式，相加即证。

内心性质的应用：过内心直线的性质

在那之前，我们要先知道： 性质4 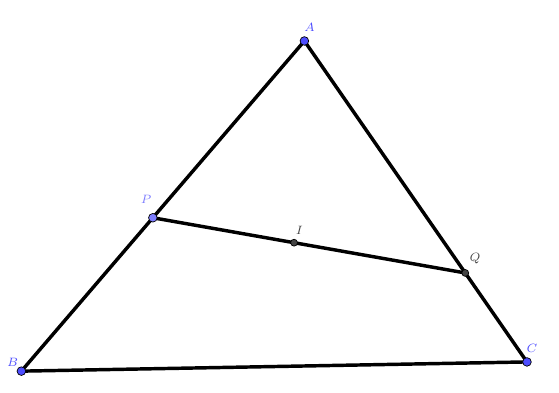如上图：过$\triangle ABC$的内心$I$任意作一条直线，分别交$AB$，$AC$于$P$及$Q$两点，则有 $$\frac{AB}{AP}\cdot AC+\frac{AC}{AQ}\cdot AB=AB+AC+BC$$ 两边同时除以$2R$，还有 $$\frac{AB}{AP}\cdot\sin\angle B+\frac{AC}{AQ}\cdot\sin\angle C=\sin\angle A+\sin\angle B+\sin\angle C$$

例题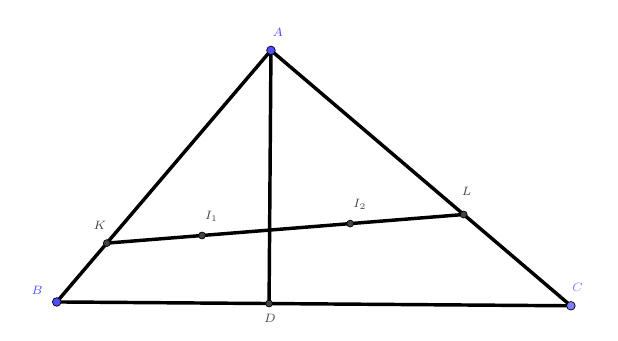： （IMO-29试题）在$Rt \triangle ABC$中，$AD$是斜边$BC$上的高，连接$\triangle ABD$的内心$I_1$和$\triangle ACD$的内心$I_2$的直线交$AB$边于$K$，交$AC$边于$L$，$\triangle ABC$与$\triangle AKL$的面积分别记为$S$和$T$，证明：$S\geqslant 2T$。

证明： 记$AD$与$KL$相交于$E$，由上面的性质4可以得到 $$\frac{AB}{AK}\cdot AD+\frac{AD}{AE}\cdot AB=AB+AD+BD$$ $$\frac{AD}{AE}\cdot AC+\frac{AC}{AL}\cdot AD=AC+AD+DC$$ 上述两个式子可以变形为： $$\frac{1}{AK}+\frac{1}{AE}=\frac{1}{AD}+\frac{1}{AB}+\frac{BD}{AB\cdot AD}$$ $$\frac{1}{AK}+\frac{1}{AL}=\frac{1}{AD}+\frac{1}{AC}+\frac{DC}{AC\cdot AD}$$ 由射影定理可知$\frac{BD}{AB\cdot AD}=\frac{1}{AC}$，$\frac{DC}{AC\cdot AD}=\frac{1}{AB}$，因此我们有$AK=AL$，即$\angle AKI_1=\angle ALI_1=45^\circ$，从而易得$\triangle AKI_1\cong\triangle ADI_1$。 从而$AK=AD$。于是$\frac{S}{T}=\frac{AB\cdot AC}{AK\cdot AL}=\frac{AB}{AD}\cdot\frac{AC}{AD}=\frac{1}{\sin\angle B}\cdot\frac{1}{\sin\angle C}=\frac{1}{\sin\angle B}\cdot\frac{1}{\cos\angle B}$ $=\frac{2}{\sin 2\angle B}\geqslant 2$，故$S\geqslant 2T$，证毕。 （注：以上解法来自孙哲《三角形内心的一个性质与三道几何名题的新证》（《中学数学》1999年第6期））

习题

（欢迎大家投稿补充！）  

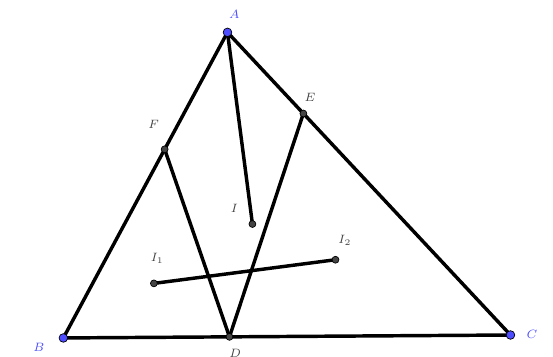$I$是$\triangle ABC$的内心，$D$、$E$、$F$是$A$、$B$、$C$在对边上的射影，$I_1$、$I_2$分别是$\triangle BDF$和$\triangle CDE$的内心，证明：$AI\perp I_1I_2$。

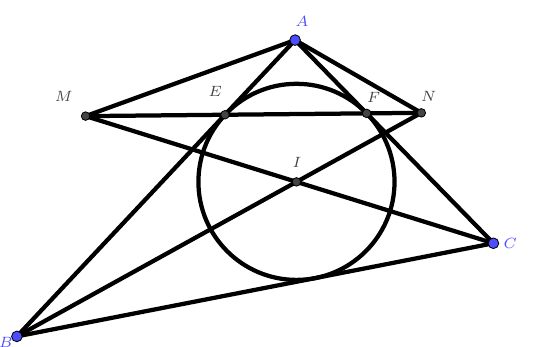设$\triangle ABC$的内切圆$I$与$AB$、$AC$边分别切于$E$、$F$，射线$BI$、$CI$分别交$EF$于点$M$、$N$，求证：四边形$AMIN$与三角形$IBC$的面积相等。

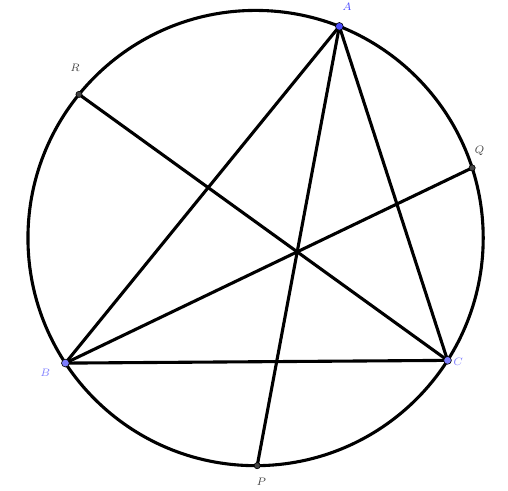在$\triangle ABC$中，$\angle A$、$\angle B$、$\angle C$的平分线分别交外接圆于$P$、$Q$、$R$，求证：$AP+BQ+CR>BC+CA+AB$。