三角形的重心

三角形的重心的性质

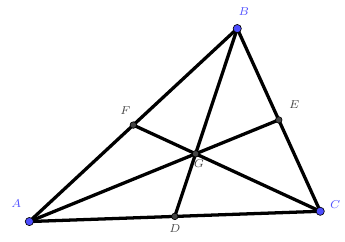
三角形的重心（一般用字母$G$表示），是三角形三条中线的交点，如下图。 重心作为一个特殊点，有什么特殊的性质呢？ 性质1 重心到一边中点的距离是这条边上中线的长的三分之一。如上图，我们有$BD=3GD，CF=3GF，AE=3GE$。 性质2 若$G$为$\triangle ABC$的重心，则$S_{\triangle ABG}=S_{\triangle BCG}=S_{\triangle CAG}=\frac{1}{3}S_{\triangle ABC}，反之亦然$。 性质3（严格来讲这不能算重心的性质，不过在这里也讲一下吧） ——中线长公式 在上图中，我们有$BD^2=\frac{1}{2}AB^2+\frac{1}{2}BC^2-\frac{1}{4}AC^2$。该公式揭示了中线的长度与三角形三边长度的关系。这个东西的证明方法相信大家都已经会了。

到现在，我们能初步发现，关于重心的性质大都围绕着边和面积，因此单纯与重心有关的难题大多需要复杂的边和面积的计算（此时我们伟大bjq负责的代数在几何中的重要性就体现了），即使是关于重心的简单题目，也要先往导边和面积法的方向上走一走。

有意思的东西——莱布尼兹公式

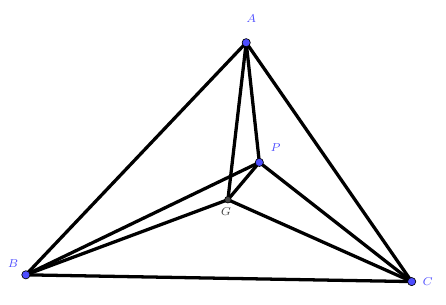在上图中，我们有$AP^2+BP^2+CP^2=3PG^2+\frac{1}{3}(AB^2+BC^2+CA^2)$.这个结论对$\triangle ABC$中任意一点$P$都成立。 如何证明呢？我们需要证明两个分结论： $$AP^2+BP^2+CP^2=AG^2+BG^2+CG^2+3PG^2$$ $$GA^2+GB^2+GC^2=\frac{1}{3}(AB^2+BC^2+CA^2)$$ 先来证明第一个结论。

上图中，$D$为$BC$边上的中点，由余弦定理，我们有$AP^2=AG^2+PG^2-2AG\cdot PG\cdot\cos\angle AGP，PD^2=DG^2+PG^2-2DG\cdot PG\cdot\cos\angle DGP$，而$AG=2DG，\cos\angle AGP=-\cos\angle DGP$，于是，1式+2式+2式，我们有$AP^2+2PD^2=AG^2+2DG^2+3PG^2$。 又由中线长公式，我们有$2PD^2=PB^2+PC^2-\frac{1}{2}BC^2，2DG^2=BG^2+CG^2-\frac{1}{2}BC^2$，代入上式就能得到$AP^2+BP^2+CP^2=AG^2+BG^2+CG^2+3PG^2$。

再来证明第二个结论。

实际上，由中线长公式和重心的性质，我们有$\frac{9}{4}AG^2=\frac{1}{2}AB^2+\frac{1}{2}AC^2-\frac{1}{4}BC^2，\frac{9}{4}BG^2=\frac{1}{2}AB^2+\frac{1}{2}BC^2-\frac{1}{4}AC^2，\frac{9}{4}CG^2=\frac{1}{2}BC^2+\frac{1}{2}AC^2-\frac{1}{4}AB^2$。三个式子相加整理即证。

由上，我们证明了莱布尼兹公式和两个比较有用的结论。通过上面的证明，我们已经看到了计算（尤其是中线长公式）在重心有关问题中的应用次数。 除了上面两个结论之外，我再补充一个结论： $$BC^2+3GA^2=CA^2+3GB^2=AB^2+3GC^2=2(AG^2+BG^2+CG^2).$$

重心性质的应用——线段比例的转化

例题1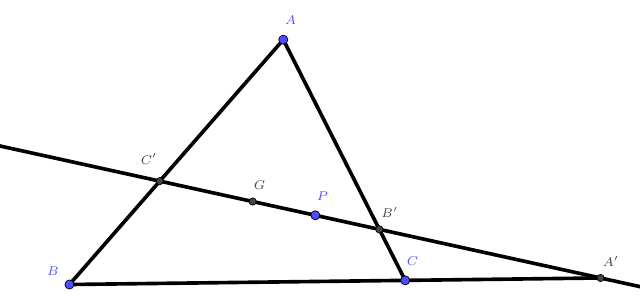： 在$\triangle ABC$中，$G$为重心，$P$为形内一点，直线$PG$交直线$BC$、$CA$、$AB$于$A’，B’，C’$，求证:$\frac{A’P}{A’G}+\frac{B’P}{B’G}+\frac{C’P}{C’G}=3$。 提示：遇到三个式子相加等于某个式子，而这些式子用平常的方法难以做变换时，可以考虑面积法。

证明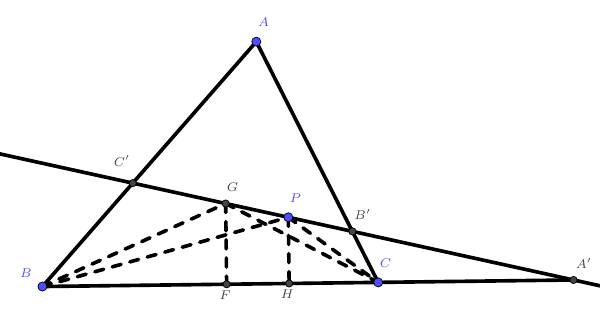： 如上图作辅助线，其中$GG’\perp BC，PP’\perp BC$。 从而$GG’//PP’，\frac{PP’}{GG’}=\frac{A’P}{A’G}$。因为$\frac{S_{\triangle PBC}}{S_{\triangle GBC}}=\frac{PP’}{GG’}$，所以$\frac{S_{\triangle PBC}}{S_{\triangle GBC}}=\frac{A’P}{A’G}$。 同理，我们可以得到$\frac{S_{\triangle PCA}}{S_{\triangle GCA}}=\frac{B’P}{B’G}，\frac{S_{\triangle PAB}}{S_{\triangle GAB}}=\frac{C’P}{C’G}$。 因为G为重心，所以$S_{\triangle GAB}=S_{\triangle GBC}=S_{\triangle GCA}$，从而将上面三个式子相加即证。

Tips：除了用面积法转化线段比例，我们还可以使用相似和平行线。

例题2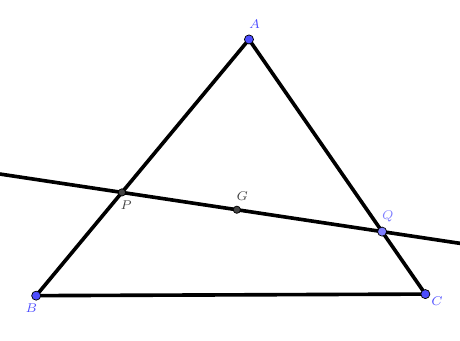： 在$\triangle ABC$中，$G$为重心，过$G$的直线交$AB$于$P$，交$AC$于$Q$，证明：$\frac{AB}{AP}+\frac{AC}{AQ}=3$。 提示：转化线段比例，平行线与相似首先要考虑。 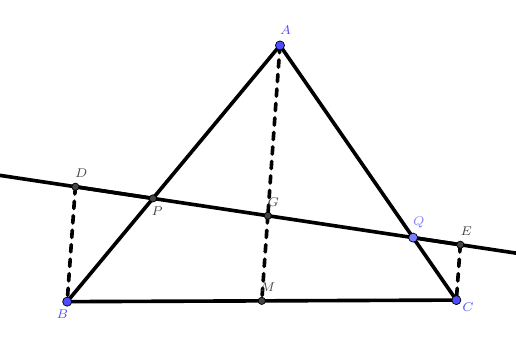证明：如图作辅助线，其中$BD//AM//EC$ 证明原命题相当于证明$\frac{PB}{AP}+\frac{QC}{AQ}=1$。 因为$\frac{PB}{AP}=\frac{DB}{AG}，\frac{QC}{AQ}=\frac{EC}{AG}$，所以只要证明$PB+QC=AG$。而因为$GM$是梯形$DBCE$的中位线，所以$PB+QC=2GM=AG$，证毕。

重心性质的应用——中线长公式

例题1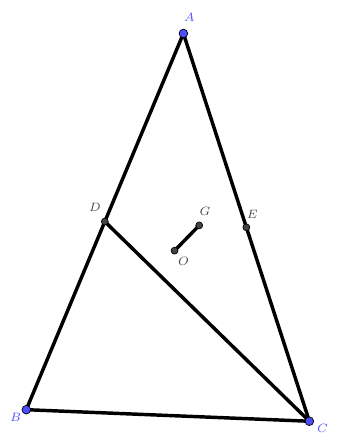： 设$O$为$\triangle ABC$的外心，$AB=AC$，$D$是$AB$的中点，$G$是$\triangle ACD$的重心，求证：$OG\perp CD$. 证明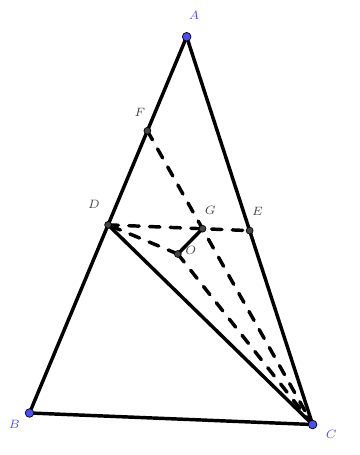： 如图作辅助线。要证明$OG\perp CD$，只要证明$DG^2-GC^2=DO^2-OC^2$. 由中线长公式和重心性质，$LHS=\frac{4}{9}DE^2-\frac{4}{9}GC^2=\frac{4}{9}(\frac{1}{2}AD^2+\frac{1}{2}AC^2-\frac{1}{4}AD^2)-\frac{4}{9}(\frac{1}{2}DC^2+\frac{1}{2}AC^2-\frac{1}{4}AD^2)=\frac{2}{9}AD^2+\frac{2}{9}DC^2-\frac{1}{9}AC^2-\frac{2}{9}DC^2-\frac{2}{9}AC^2+\frac{1}{9}AD^2=\frac{1}{3}AD^2-\frac{1}{3}AC^2=-AD^2$. 而$RHS=DO^2-OC^2=DO^2-AO^2=DO^2-(OD^2+AD^2)=-AD^2$. 所以$LHS=RHS$，证毕。 例题2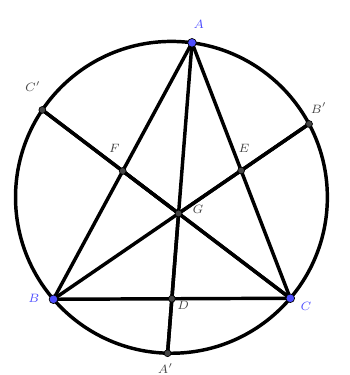： 设$\triangle ABC$的重心为$G$，$AG$，$BG$，$CG$，分别交对边于$D$，$E$，$F$，交$\triangle ABC$的外接圆于$A’$，$B’$，$C’$，求证：$\frac{A’D}{DA}+\frac{B’E}{EB}+\frac{C’F}{FC}\geqslant 1$. 证明：设$BC=a$,$CA=B$,$AB=c$，这三边上的中线分别记为$m_a$,$m_b$,$m_c$。 由相交弦定理，我们有$\frac{A’D}{DA}=\frac{A’D\cdot DA}{DA^2}=\frac{BD\cdot DC}{DA^2}=\frac{a^2}{4m_a^2}$。 对其余两个式子做相同的操作，我们可知要证明原命题，我们只要证明： $$\frac{a^2}{m_a^2}+\frac{b^2}{m_b^2}+\frac{c^2}{m_c^2}\geqslant 4$$ 由三角形的中线长公式，我们易知$a^2=\frac{4}{9}(2m_b^2+2m_c^2-m_a^2),b^2=\frac{4}{9}(2m_c^2+2m_a^2-m_b^2),c^2=\frac{4}{9}(2m_a^2+2m_b^2-m_c^2)$，代入左式即知不等式成立。

习题

（欢迎大家投稿补充！）

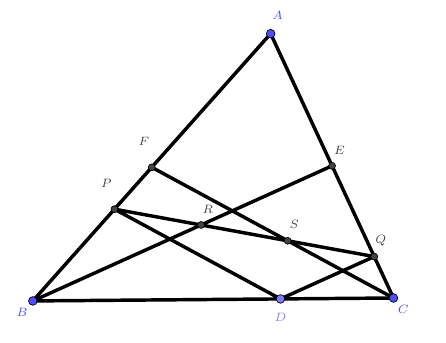在$\triangle ABC$中，设$E$，$F$分别为$AC$，$AB$的中点，$D$为$BC$上任一点，$P$,$Q$两点分别满足$DP//CF$，$DQ//BE$，$PQ$交$BE$于$R$，交$CF$与$S$。求证：$PQ=3RS$.

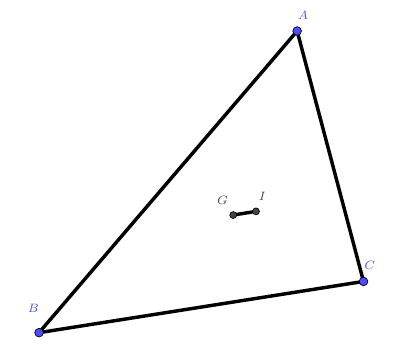已知$\triangle ABC$的重心$G$和内心$I$的连线$GI//BC$。求证：$AB+AC=2BC$

3.证明：如果三角形的三边的平方成等差数列，那么该三角形和由它的三条中线围成的新三角形相似。